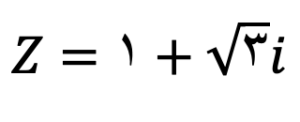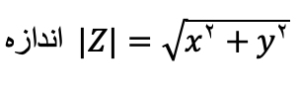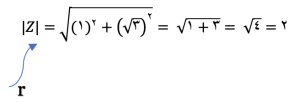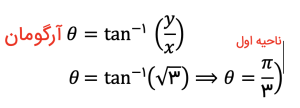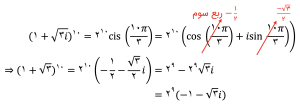قضیه دمواور در اعداد مختلط – به توان رساندن اعداد مختلط

مقدمه

قضیه دمواور، نامگذاری به افتخار ریاضیدان فرانسوی شده است. ابراهام دموآور، یکی از اصول پایه‌ای و کلیدی در مطالعه و تحلیل اعداد مختلط است.

این قضیه به خصوص در دروس دانشگاهی مثل ریاضیات عمومی ۱ و مهندسی برق از اهمیت بالایی برخوردار است و در امتحانات به طور مکرر مورد سوال قرار می‌گیرد.

قانون دمواور امکان پردازش ساده‌تر و کارآمدتر اعداد مختلط را به توان‌های بالا فراهم می‌آورد، که این خود کاربردهای فراوانی در محاسبات مهندسی، فیزیک و حتی در تحلیل‌های مالی دارد.

به طور خلاصه، این قانون راهی برای ساده‌ سازی محاسبات پیچیده در مورد اعداد مختلط است. که در غیر این صورت ممکن است بسیار زمان‌بر و خطاپذیر باشد.

مرحله صفرم: طرح سوال

مثال :

فرض کنید می‌خواهیم عدد مختلط روبرو را به توان 10 برسونیم.

مرحله اول: فرآیند قطبی کردن اعداد مختلط

قبل از اینکه بتوان از قضیه دموآور استفاده کرد، لازم است که عدد مختلط مورد نظر به شکل قطبی درآید.

در این شکل، یک عدد مختلط به جای اینکه با بخش‌های حقیقی و موهومی خود شناخته شود، با مقدار زاویه و طول بردار از مبدأ توصیف می‌شود.

1. محاسبه اندازه: اندازه یک عدد مختلط، که در آن اعداد حقیقی هستند، به صورت ریشه دوم مجموع مربعات این دو جزء محاسبه می‌شود:

2. محاسبه آرگومان: آرگومان یک عدد مختلط، که زاویه‌ای است بین خط واصل از مبدأ به نقطه نماینده عدد مختلط در صفحه مختلط، از طریق تابع آرکتانژانت به دست می‌آید.

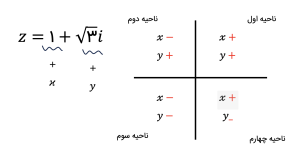
این زاویه باید با دقت انتخاب شود. زیرا بسته به اینکه عدد مختلط در کدام ناحیه قرار دارد، ممکن است نیاز به تعدیلاتی داشته باشد:

مرحله دوم: استفاده از قضیه دمواور

پس از آنکه عدد مختلط به فرم قطبی درآمد. باید از قانون دمواور برای بالا بردن این عدد به توان مورد نظر استفاده کرد.

فرمول کلی قضیه دمواور به صورت زیر است:

که در آن  r ناحیه و Θ آرگومان عدد مختلط است و  n  توان مورد نظر می‌باشد.

این فرمول به ما امکان می‌دهد که به سرعت و به آسانی اعداد مختلط را به توان‌های بالا برسانیم بدون آنکه نیازمند محاسبات دستی پیچیده‌ای باشیم.

جمع‌بندی

درک و استفاده از قانون دموآور می‌تواند به عنوان یک مهارت کلیدی در درک بهتر ریاضیات پیشرفته و همچنین در کاربردهای عملی آن در مهندسی و فیزیک ارزشمند باشد.

استفاده از این قانون در تحلیل‌های مهندسی به ویژه در زمینه‌هایی مانند الکترومغناطیس، دینامیک سیستم‌ها و مکانیک کوانتومی بسیار مفید است.

درک این که چگونه اعداد مختلط می‌توانند به شکل‌های مختلفی مانند قطبی و دکارتی نمایش داده شوند، به شما امکان می‌دهد که با اعداد و مفاهیم پیچیده‌تر به روشی ساده‌تر کار کنید.

از تخفیف های داخل کانال جزوه جو غافل نشوید.