مقدمه:
از آنجایی که مسائل ترسیمی از دیرباز نقش مهمی در هندسه و ریاضیات داشته اند، یونانیان باستان اغلب وقت خود را صرف حل مسائل ترسیمی هندسه میکردند. و در این بین گاهی با چالش هایی روبرو میشدند، که اصلا ساده نبود؛ از جمله این چالش ها رویارویی با مسائلی بود، که حل آنها دشوار،زمانبر یا در برخی موارد حتی غیرممکن بود.
سه مسئله حل نشده ریاضی در عهد باستان کدام بودند؟
تثلیث زاویه، تربیع دایره و تضعیف مکعب سه مسئلهی مشهور غیر قابل حل در ریاضیات هستند. که از آنها تحت عنوان مسائل سه گانه عهد باستان یاد میشود.
به طور کلی، با سیر تکامل علم ریاضی و با همت و کوشش های فراوان دانشمندان مختلف عدم امکان حل این مسائل اثبات شده است.
در این مقاله از سری مقالات جزوه جو قصد داریم هر یک ازین مسائل سه گانه را به تفکیک بررسی کنیم.

قبل از مطالعه ی مقاله بهتر است با اصطلاحات زیر آشنا شوید:
سَتاره: وسیله ای که به کمک آن تنها میتوان یک خط راست رسم کرد اما نمیتوان طول چیزی را اندازه گرفت. یعنی اگر دو نقطه در اختیار داشته باشیم با کمک ستاره میتوان آنها را با رسم یک خط راست به هم وصل کرد. اما نمیتوان به طور مثال پاره خطی به طول پنج سانتیمتر رسم کرد. به بیان ساده ستاره همان خطکش غیر مدرج است.
پرگار فروریختنی: پرگاری که به کمک آن تنها میتوان به مرکز یک نقطه دایره ای رسم کرد که از نقطه ی دیگر بگذرد. این وسیله که تحت عنوان پرگار اقلیدس نیز شناخته میشود کمی با پرگار های امروزی متفاوت است. به طوریکه نمیتوان دهانه ی پرگار را به اندازه ی یک پاره خط باز کرد. و سپس به مرکز نقطه ای از در جای دیگر از صفحه، دایره ای با آن شعاع رسم کرد. اصطلاحا گفته میشود که پرگار اقلیدس فروریختنی است. یعنی به محض اینکه از روی کاغذ برداشته شود قطر دهانه ی آن تغییر میکند.
اولین مسئله حل نشده ریاضی: تثلیث زاویه
آیا میتوان فقط به کمک یک ستاره و پرگار هر زاویه ای را به سه قسمت مساوی تقسیم کرد؟
یکی از سه مسئله ی مشهور هندسه ی یونان باستان،مسئله ی تقسیم زاویه به سه بخش مساوی فقط با استفاده از پرگار و ستاره است.
به طور کلی بزرگان ریاضی در طول دوران قادر بودند به راحتی و با رسم نیمساز، هر زاویه ی دلخواه را به دو قسمت مساوی تقسیم کنند. درحالیکه در تقسیم یک کمان به سه قسمت مساوی عاجز بودند. بنابراین مسئله ی مشهور تثیلث زاویه تبدیل به یکی از مسائل غیرقابل حل یونان باستان شده است. اگر اندکی با مثلثات آشنایی داشته باشید. میتوانید اثبات غیرممکن بودن این مسئله را به سادگی درک کنید. جالب است بدانید که اگرچه غیرممکن بودن حل این مسئله برای حالت کلی اثبات شده است. با این وجود تثلیث برخی زوایا امکان پذیر است. قضیه ای وجود دارد که به کمک آن میتوان زوایای قابل تثلیث را پیدا کرد.
روش حل تثلیث زاویه
قضیه: زاویه ی θ میتواند تثلیث شود اگر و تنها اگر چندجمله ای زیر بر روی توسیع میدان Q(cos(θ)) تحویل پذیر(قابل حل)باشد.
در این قضیه Q نماد مجموعه اعداد گویا است.
از این قضیه میتوان نتیجه گرفت که با حل یک معادله ی درجه 3 ساده میتوانیم بینهایت زاویه پیدا کنیم، که باکمک ابزار های مذکور قابل تثلیث هستند. مشهورترین آنها 90 و 45 درجه هستند. از طرفی میتوان دریافت که بینهایت زاویه وجود دارد. که تثلیث آنها غیرممکن است؛ازجمله 60 درجه. (اگر شما هم در ریاضیات دچار مشکل هستید حتما دوره کارگاه مشتق و انتگرال را از دست ندهید.)
به طور کلی تاکنون برای این مسئله جواب قانع کننده ای که از سوی آکادمی بین المللی ریاضی قابلیت تایید را داشته باشد. ارائه نشده و عدم امکان حل آن برای حالت کلی را میتوان اثبات شده در نظر گرفت.
در شکل زیر تثلیث زاویه ی θ به کمک پرگار و ستاره نشان داده شده است.
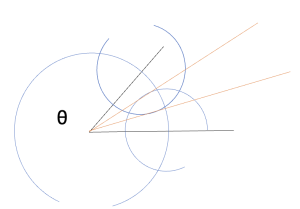
نکته: این قضیه که تثلیث زاویه مسئله ای غیرقابل حل است. تنها زمانی صادق است که ابزاری که در اختیار داریم محدود به پرگار فروریختنی و ستاره باشد؛ زیرا ما میدانیم که در صورتی که استفاده از ابزار های دیگر مجاز باشد. مجموعه ترسیم های ممکن بسیار گسترده تر خواهد بود.
دومین مسئله حل نشده ریاضی : تربیع دایره
آیا میتوان به ازای هر دایره ی دلخواه مربعی هم مساحت با آن رسم کرد؟
تربیع دایره دومین مسئله ی مشهور هندسهی یونان باستان است. که عبارت است، از یافتن مربعی که مساحت آن برابر با مساحت دایره ی مفروض باشد.
ایده ی شکل گیری این مسئله از آنجا بود که ریاضی دانان یونان باستان از دیرباز مساحت هرشکل را برحسب شکلی دیگر بیان میکردند.در نتیجه در صدد آن برآمدند تا روشی ارائه کنند که به کمک آن بتوان برای هر دایره ی مفروض مربعی هم مساحت با آن رسم کرد. بیان بهتر مسئله ی تربیع دایره به معنای یافتن رابطه ای برای مساحت دایره برحسب قطر و شعاع آن است.
و اما موضوعی که مسئله ی تربیع دایره را از دو مسئله ی دیگر متمایز میکند. این است که علاوه بر ریاضی دانان، فلاسفه نیز به بحث و گفتگو درباره ی آن پرداخته اند. علاوه بر این، تربیع دایره به طور مستقیم با عدد پی (π) در ارتباط است.
در طی قرون 3 تا 5 قمری دانشمندان زیادی به تفکر درباره ی این مسئله پرداخته اند. که مشهورترین آنها را به طور مختصر بررسی میکنیم:

بروسون:
به طور کلی میتوان هر دایره را به مثلث هایی تجزیه کرد. سپس میتوان به ازای هر مثلث، مربعی مساوی با آن پیدا کرد. درنتیجه یافتن مربعی که مساوی با مجموع این مثلث ها باشد. نیز امکان پذیر است. و این به معنای حل مسئله ی تربیع دایره خواهد بود.
برهان رد استدلال: ضلع مربعی که بروسون به آن اشاره میکند. و طبق استدلالش معادل دایره است، درواقع تنها وجود بالقوه دارد. و به وجود آن به صورت بالفعل اثبات نشده است.
ابن سینا نیز معتقد بود که استدلال بروسون هندسی نیست. بلکه جدلی یا منطقی است و به همین جهت اصطلاحا “خارجی” به شمار می آید. پس این مسئله ریاضی حل نمیشود.
استدلال بقراط:
برای درک بهتر این استدلال لازم است. ابتدا بدانیم که بقراط خیوسی موفق به رسم مربعی هم مساحت با نوع خاصی از ماهک (شکل هلالی محصور به دو کمان دایره) شده بود.
استدلال بقراط به این صورت بیان میشود که دایره مساوی با مجموعه ای از شکل های مستقیم الخط است. و هرچه مساوی با شکل های مستقیم الخط باشد، قابل تربیع است. درنتیجه دایره نیز قابل تربیع است. از طرفی چون اثبات شده است که به ازای هلال های بخصوص میتوان مربع هم مساحت رسم کرد، میتوان نتیجه گرفت. با تقسیم دایره به مجموعه ای از این هلال ها،دایره تربیع پذیر است.
برهان رد استدلال: ابن سینا این استدلال را نیز به این شکل رد میکند: دایره تماما قابل تقسیم به شکل های هلالی نیست. و در هر صورت شکل های غیرهلالی از آن باقی میماند. به عبارتی نسبت هلال واره ها به دایره مثل نسبت جز به کل است،نه نسبت جزئی به کلی. یعنی هلال واره ها اجزای دایره هستند. نه دایره هایی که تحت نوع کلی دایره قرار بگیرند.
استدلال آنتیفون:
اگر مربعی را به صورت محاط در دایره قرار دهیم. سپس وسط های هر کمان متناظر به هر ضلع مربع را به دوسر آن کمان وصل کنیم و به تکرار اینکار به اندازه ی کافی ادامه دهیم. به جایی میرسیم که به جای یک مربع درون دایره، یک چند ضلعی منتظم داریم که چندان تفاوتی با دایره ی ابتدایی ندارد. چون هر چندضلعی منتظم تربیع پذیر است. پس دایره نیز تربیع پذیر است.
برهان رد استدلال:
با اینکه استدلال آنتیفون به نظر منطقی تر از سایر استدلال ها می آید. اما اصلی ترین ایرادی که به آن وارد میشود این است که این روش مسئله را به صورت تقریبی حل میکند. ضمن اینکه در آن زمان نیز افراد شکاکی وجود داشتند. که استدلال میکردند که اندازهها را نمیتوان بدون محدودیت تقسیم کرد. بنابراین مساحت دایره هرگز پر نمیشود. پس این مسئله حل نشده ریاضی باقی ماند.
به نظر می آید آنتیفون بر این باور بوده است که خط مماس بر یک دایره آن را در یک نقطه قطع نمیکند. بلکه همانطور که با چشم میبینیم، دایره و خط مماس چندین نقطه ی مشترک دارند.
غیر قابل حل بودن این مسئله در نهایت در سال 1882 میلادی توسط فردیناند لیندمان ، ریاضیدان آلمانی با اثبات غیرجبری بودن عدد پی (π) اثبات شد. غیرجبری بودن عدد پی ثابت میکند که امکان تربیع دایره به طور دقیق وجود ندارد.
اثبات وی به این صورت بیان میشود که عدد پی یک عدد غیر جبری یا متعالی است. به این معنا که نمیتواند ریشه ی یک معادله ی جبری با ضریب های صحیح باشد. بنابراین مسئله تربیع دایره نه تنها با خط کش و ستاره، بلکه با سایر منحنی های جبری مانند مقاطع مخروطی نیز قابل حل نیست.

البته بعدها ریاضیدان مجارستانی به نام یانوش بویویی موفق شد. نشان دهد که تربیع دایره برای برخی دایره ها در هندسه ی نااقلیدسی ممکن است. زیرا مساحت این دایره ها برابر با π2 است. که در آن پی عدد متغیری وابسته به شعاع دایره است.
سومین مسئله حل نشده ریاضی : تضعیف مکعب
آیا میتوان به ازای هر مکعب دلخواه،مکعبی رسم کرد که حجم آن دوبرابر مکعب مفروض باشد؟
سومین و آخرین مسئله ی لاینحل از دوران باستان که در این مقاله ذکر میکنیم. مسئله ی تضعیف مکعب است. که موضوع آن یافتن ضلع مکعبی است که حجم آن دوبرابر مکعب مفروض باشد.
منظور از تضعیف،همان مضاعف کردن یا دوبرابر کردن هر مکعب مفروض است.
ظاهرا میتوان سرچشمه ی تضعیف مکعب را در تمایل ریاضیدانان باستانی به تعمیم مسئله ی ساده ی دوبرابر کردن مربع دانست.
برای حل این مسئله نیز، مانند مسائلی که پیشتر مطرح شد. راه حل های مختلفی در ادوار مختلف توسط دانشمندانی از سراسر جهان پیشنهاد شده است. که با توجه به پیچیدگی و طولانی بودن آنها در این مقاله پوشش داده نمیشوند.
تنها چیزی که قصد داریم در اینجا بیان کنیم. اثبات عدم امکان حل این مسئله به صورت خلاصه و ساده است.
مسئله را به صورت خیلی ساده در نظر بگیریم:
فرض کنید مکعبی به طول ضلع 1 در اختیار داریم؛میدانیم که حجم این مکعب برابر است با:
حال اگر بخواهیم حجم این مکعب را تضعیف کنیم:
2×1=2
بعد از تضعیف حجم مکعب باید ضلع مکعب جدید را بدست آوریم. بدیهی است که برای بدست آوردن ضلع مکعب جدید باید از حجم آن ریشه ی سوم بگیریم؛در نتیجه:
عدد رادیکال دو با فرجه ی سه یک عدد گنگ است.کافی است ثابت کنیم که این عدد(اندازه ی ضلع مکعب جدید) با ابزاری که در دست داریم قابل ترسیم است یا خیر.
برای پاسخ به این سوال ابتدا باید بدانیم که چه اعدادی با ستاره و پرگار مذکور قابل رسم هستند.
عدد ترسیم پذیر:
در جبر و هندسه عدد حقیقی r را ترسیم پذیر گوییم، اگر و تنها اگر بتوان با داشتن پاره خط واحد،با خط کش و پرگار در تعداد مراحل متناهی پاره خطی به طول |r| رسم کرد. به بیان جبری یک عدد ترسیم پذیر است. اگر و تنها اگر بتوان آن را با اعمال مراحل متناهی چهار عمل اصلی و ریشه ی دوم آن(فقط ریشه ی دوم و نه ریشه های بالاتر)بر اعداد ترسیم پذیر دیگر ساخت. بنا بر تعریف 0 و 1 ترسیم پذیر اند.
طبق تعریف به وضوح مشاهده میشود که عدد بدست امده یک عدد ترسیم پذیر نیست،درنتیجه تضعیف مکعبی با ضلع 1 امکان پذیر نیست.
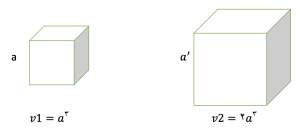
و اما رسم مکعب با اندازه ی ضلع a چطور؟
معکبی با ضلع a داریم و میخواهیم آن را تضعیف کنیم. اگر حجم مکعب مورد نظر را v1 ، حجم مکعب تضعیف شده را v2 و ضلع آنرا در نظر بگیریم. خواهیم داشت:
بنابراین ضلع مکعب تضعیف شده برابر است با:
همانطور که میبینید باید a را در رادیکال 2 با فرجه 3 ضرب کنیم که عددی ترسیم ناپذیر است؛در نتیجه مکعب با ضلع a ترسیم ناپذیر است.
پ.ن:جالب است بدانید با وجود اثبات غیرممکن بودن حل این مسائل،هنوز عده ای در حال تلاش برای ارائه ی راه حل قطعی برای آن ها هستند.
برای اطلاع از تخفیف های ما به کانال جزوه جو در تلگرام مراجعه کنید.
گردآورنده: هانیه اکرمی


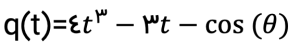
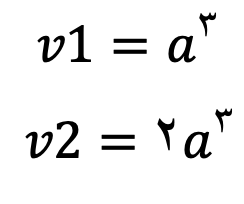
خیلی عالی❤️
خوشحالیم که برای شما مفیده بوده.
خیلی کوتاه و مفید🙏
متشکریم از دیدگاه شما.
عالی👌👌
🙏🏻🙏🏻 ممنون