معکوس کردن ماتریسها یکی از مفاهیم کلیدی در جبر خطی است که در بسیاری از محاسبات مهندسی و علمی کاربرد دارد.
معکوس ماتریس های ۳*۳ در درس ریاضی عمومی ۲ آمده و چالش های زیادی را برای دانشجویان بوجود آورده است.
اگر در درس ریاضی عمومی ۲ مشکل دارید و نمیدونید از کجا باید شروع کنید، پیشنهاد میکنم از دوره ریاضی عمومی ۲ جزوه جو غافل نشید.
در این مقاله، ما به شما نحوه معکوس کردن یک ماتریس ۳x۳ را به صورت مرحله به مرحله آموزش خواهیم داد.
مرحله صفر: فرض مثال ماتریس ۳*۳
فرض کنید ماتریس زیر را میخواهیم معکوس کنیم.
مرحله ۱: محاسبه کهاد ماتریس
ابتدا، باید کهاد ماتریس را برای هر عنصر ماتریس اصلی را محاسبه کنیم. کهاد ماتریس به معنای محاسبه دترمینان برای هر ۲x۲ ماتریسی است که از حذف سطر و ستون مربوط به عنصر مورد نظر به دست میآید. برای مثال، اگر ماتریس اصلی ما به صورت زیر باشد:
برای محاسبه کهاد عنصر اول (1)، سطر اول و ستون اول را حذف میکنیم و دترمینان ماتریس باقیمانده را محاسبه میکنیم:
این کار را برای تمام عناصر ماتریس انجام میدهیم.
مرحله ۲: محاسبه ماتریس همسازه برای معکوس کردن
پس از به دست آوردن کهاد ماتریس، نوبت به محاسبه ماتریس همسازه میرسد. یعنی ماتریس کهاد ساخته شده رو در ماتریس مثبت و منفی ضرب کنید.
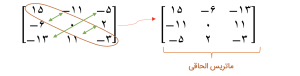
مرحله ۳: ساخت ماتریس الحاقی
برای ساخت این ماتریس دست به قطر ماتریس نمیزنیم و بقیه عناصر رو با عناصر رو به روی خود جا به جا میکنیم.
مرحله ۴: ضرب کردن در معکوس دترمینان
آخرین گام، ضرب ماتریس الحاقی در معکوس دترمینان ماتریس اصلی است. ابتدا دترمینان ماتریس A را محاسبه میکنیم:
دترمینان ماتریس ۳ در ۳ به این صورت است:
سپس، هر عنصر ماتریس الحاقی را در دترمینان ماتریس ۳*۳ ضرب میکنیم تا ماتریس معکوس به دست آید.
با این روش، میتوانید ماتریسهای ۳x۳ را به راحتی معکوس کنید و در محاسبات پیچیدهتر که نیاز به معکوس ماتریس دارند، از آن استفاده نمایید. این دانش در بسیاری از زمینههای علمی و مهندسی کاربردی است و میتواند در درک بهتر سیستمها و حل مسائل مختلف به شما کمک کند.
برای اطلاع از تخفیف ها و دوره های آموزشی کانال ما رو دنبال کنید.

محسن شریفی پویا
مدرس ریاضیات پایه و دانشگاهی




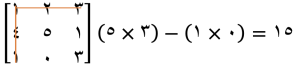
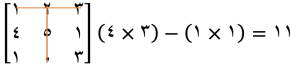
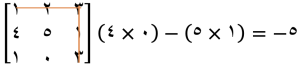
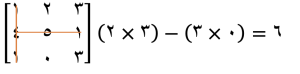
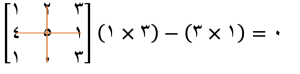
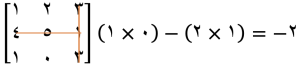
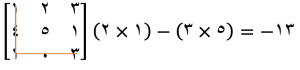
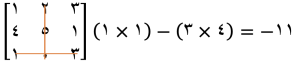
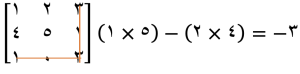
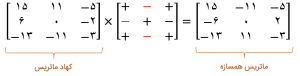
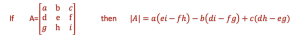
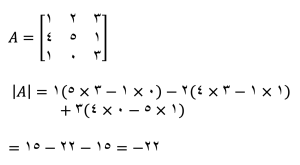

ببخشید نقش کهاد چی بود این وسط؟
از ماتریس کهاد ماتریس همسازه بدست میاد و ماتریس همسازه تبدیل به الحاقی میشه و در نهایت معکوس دترمینان در الحاقی ضرب میشه. پس بدست آوردن ماتریس کهاد قدم اوله و بدون اون بقیه موارد بدست نمیاد
چقدر خوب و کامل و روان توضیح داده بودین ، سپاس از شما