دنباله ی اسرار آمیز فیبوناچی
مقدمه
متاسفانه اغلب ما به این دلیل اولین بار شروع به یادگرفتن ریاضی کردیم که اصطلاحا “در امتحان می آید.”.
اما واقعیت این است که حتی اگر اندکی سعی کنیم با علم ریاضی به دلیل زیبایی و ظرافت آن آشنا شویم، یا حتی درباره ی کاربرد های آن در زندگی روزمره بدانیم، متوجه میشیم که ریاضی علم شگفتی هاست و هرچه بیشتر درباره آن بدانیم بیشتر به عمق زیبایی ، ظرافت و جذابیت آن پی میبریم.
ضمن اینکه میتوان به جرات ادعا کرد که بدون پیشرفت علم ریاضی پیشرفت در سایر علوم نیز هرگز ممکن نبود.
در این مقاله از سری مقالات جزوه جو سعی داریم به بررسی یکی دیگر از شگفتی های ریاضیات یعنی دنباله ی اسرارآمیز فیبوناچی و ارتباط جالب آن با طبیعت بپردازیم.
دنباله ی فیبوناچی چیست؟
همانطور که از اسم آن پیداست، اعداد فیبوناچی به صورت دنباله ی ریاضی تعریف میشوند.
به این معنا که دو ویژگی اصلی یک دنباله را دارا هستند:
1.تکرار اعضا مجاز است.
2.ترتیب اعضا اهمیت دارد.
دنباله ی فیبوناچی از الگوی بسیار ساده ای پیروی میکند:
به غیر از دو جمله اول، هر جمله از مجموع دو جمله ی قبلی بدست می آید،به بیان ریاضی:
F(n)=F(n-1)+F(n-2)
به طوری که شروع دنباله با 0 و 1 است، و سپس مابقی جملات از الگوی مذکور پیروی میکنند.
البته برخی ریاضی دانان عدد 0 را جزو این دنباله به حساب نمی آورند.(یا حداقل آن را جمله ی صفرم دنباله مینامند.) و معتقدند اولین جمله ی این دنباله عدد 1 میباشد.
در زیر چند جمله ی اول این دنباله را مشاهده میکنید:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…
با توجه به توضیحات گفته شده میتوانیم جمله ی صفرم تا دهم این دنباله را به صورت زیر نمایش دهیم:
F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 |
0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
F2=F0+F1=0+1=1
F3=F2+F1=1+1=2
F4=F3+F2=2+1=3
.
.
.
دنباله فیبوناچی یکی از مشهورترین و پرکاربردترین دنباله های ریاضی است.
اما چرا؟؟؟
پیدایش و معرفی دنباله فیبوناچی:
لئونارد فیبوناچی اولین ریاضیدان بزرگ اروپا در قرن سیزدهم میلادی بود.
پس از آنکه فیبوناچی این دنباله را به همراه اطلاعات ریاضی دیگر،که در سفر های متعددش به کشور های مختلف جمع آوری کرده بود، رسما معرفی کرد، این دنبال به افتخار وی با نام او نامگذاری شد.گویا اولین موضوعی که وی را به سمت کشف این اعداد سوق داد، مسئله ی مشهور خرگوش هایی بود که توسط خودش معرفی شد.
مسئله مشهور خرگوش های فیبوناچی:
فرض کنيد که يک جفت خرگوش نر و ماده(تازه متولد شده) داریم که در پايان هر ماه يک جفت خرگوش نر و ماده جديد بدنيا بياورند.
خرگوش ها پس از یک ماه بالغ میشوند و دوران بارداری آن ها نیز یک ماه است.هنگامی که خرگوش ماده به سن بلوغ میرسد باردار میشود و در هربار بارداری خود یک خرگوش نر و ماده به دنیا می آورد.
اگر هيچ خرگوشي نمیرد،در پايان يک سال (یا به عبارتی n ماه)چند خرگوش نر و چند خرگوش ماده وجود دارد؟؟؟
این مسئله هم به صورت تحلیلی (استفاده از فرمول ریاضی برای محاسبه ی تعداد خرگوش ها در هر ماه) و هم به صورت بازگشتی (استفاده از تابع بازگشتی برای محاسبه ی تعداد خرگوش ها در هر ماه) قابل حل است.
اما بیایید حل این مسئله را خیلی ساده شروع کنیم:
میدانیم که تعداد خرگوش ها در ماه اول برابر یک جفت است؛ اما به این جهت که بلوغ خرگوش ها برای زاد و ولد (طبق فرضیه)به یک ماه زمان نیاز دارد، پس تعداد خرگوش ها در ماه دوم نیز برابر یک جفت خواهد بود.
پس از ماه دوم خرگوش ها بالغ شده اند و یک جفت خرگوش نر و ماده جدید به دنیا می آورند.
در انتهای ماه سوم خرگوش هایی که تازه متولد شده اند آماده ی زاد و ولد میشوند و یک جفت خرگوش نر و ماده به دنیا می آورند، از طرفی خرگوش های ماه اول نیز یک جفت خرگوش نر و ماده ی جدید به دنیا می آورند.
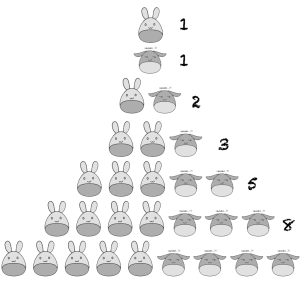
میتوان تعداد خرگوش ها در انتهای هرماه را به شکل زیر نمایش داد:
5 | 4 | 3 | 2 | 1 | ماه |
5 | 3 | 2 | 1 | 1 | تعداد جفت خرگوش ها |
با ادامه دادن این روند در میابیم که الگوی محاسبه ی تعداد خرگوش ها به صورت زیر است:
برای محاسبه ی تعداد خرگوش ها در هر ماه باید تعداد خرگوش هایی که تازه متولد میشوند را با تعداد خرگوش هایی که از قبل موجود بودند جمع کرد.(همان الگوی دنباله ی فیبوناچی)!
بدین ترتیب لئونارد فیبوناچی موفق شد با حل این مسئله به دنباله ای شگفت انگیز از اعداد دست پیدا کند که امروزه تحت عنوان دنباله ی فیبوناچی شناخته شده است.
*نکته: البته گفته میشودکه فیبوناچی اولین کسی نبود که این اعداد را کشف کرد و به اسرار آمیز بودن این اعداد پی برد، بلکه این اعداد قرن ها پیش از وی در هندوستان شناخته شده و مورد استفاده قرار گرفته اند.
ویژگی های اعجاب انگیز دنباله ی فیبوناچی:
اگر دنباله ی فیبوناچی را با دقت بیشتری بررسی کنیم، متوجه وجود خواص شگفت انگیزی در آن خواهیم شد که در اینجا به بررسی تعدادی از آنها میپردازیم.
۱.رشد سریع جملات دنباله :
این دنباله به طور نمایی رشد میکند. شاید رشد اعداد این دنباله در چندین جمله ابتدایی خیلی سریع به نظر نرسد، اما با ادامه دادن آن و بدست آوردن جملات بعدی به اعداد بسیار بزرگی دست خواهیم یافت.
2.وجود مقسوم علیه های اعداد به طور منظم در دنباله ی فیبوناچی:
اگر در در دنباله ی فیبوناچی شروع به بررسی اعداد کنیم میتوانیم مقسوم علیه های اعداد را با یک الگوی خاص بدست آوریم.
بار دیگر به اعداد دنباله توجه کنید:
N | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | … |
Fn | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
*در جمله ی 2 = F3 توجه کنید: ملاحظه میشود که هر 3 عدد بعد از این عدد یک عدد بخش پذیر بر 2 وجود دارد.
*به جمله ی F4=3 توجه کنید: ملاحظه میشود که هر 4 عدد بعد از این عدد یک عدد بخش پذیر بر 3 وجود دارد.
*جمله ی F5=5 توجه کنید: ملاحظه میشود که هر 5 عدد بعد از این عدد یک عدد بخش پذیر بر 5 وجود دارد.
الگوی بدست آمده برای یافتن مقسوم علیه ها در دنباله به این صورت تعریف میشود:
هر n عدد بعد از Fn یک عدد بخش پذیر بر n وجود دارد.
3.جملات فیبوناچی برای اعداد کوچکتر از صفر:
دنباله ی فیبوناچی برای اعداد منفی نیز قابل تعریف است.
در این صورت برای بدست آوردن اعداد دنباله از فرمول زیر استفاده میکنیم:
F-n = (-1)n+1 Fn
به طور مثال برای بدست آوردن جمله ی چهارم دنباله ی منفی فیبوناچی،به شکل زیر عمل میکنیم:
F-4 = (-1)5 .F4 = (-1) 3 = -3
۴.ترتیب قرارگیری جملات زوج و فرد در دنباله:
در دنباله ی فیبوناچی الگوی زیر برای زوج و فردبودن جملات دنباله برقرار است:
,…زوج , فرد , فرد , زوج , فرد , فرد , زوج , فرد , فرد , زوج
دلیل این امر واضح است:حاصل جمع هردو عدد فرد یک عدد زوج و حاصل جمع یک عدد فرد با یک عدد زوج، عددی فرد است.
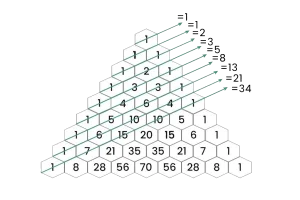
5.وجود جملات فیبوناچی در مثلث خیام پاسکال:
اگر مثلث مشهور خیام-پاسکال را به شکل ویژه قائم الزاویه رسم کنیم ،مجموع اعداد قطری، دنباله فیبوناچی را خواهد ساخت.
رابطه ی دنباله ی فیبوناچی با نسبت طلایی:
به جرات میتوان ادعا کرد که اصلی ترین ویژگی که اعداد دنباله ی فیبوناچی را تا این اندازه خاص میکند، رابطه ی آن ها با نسبت طلایی است.
به طور کلی ارتباط بین اعداد فیبوناچی و نسبت طلایی را میتوان به شیوه های مختلفی بیان کرد که در این مقاله به سه مورد از مشهورترین های آن ها میپردازیم:
دنباله ی فیبوناچی همواره به نسبت طلایی همگرا است:
نسبت طلایی یکی از مشهورترین اعداد گنگ است که برای نمایش آن از نماد φ (فی) استفاده میکنیم:
در دنباله ی فیبوناچی حاصل تقسیم هر دو عدد متوالی برابر با نسبت طلایی است.
هرچه جملات دنباله ی فیبوناچی بزرگتر باشند، حاصل تقسیم آن ها هربار نسبت طلایی را با دقت بیشتری در ارقام اعشاری به ما میدهد.
واضح است که این عدد حاصل تقسیم عدد بزرگتر به عدد کوچتر است؛یعنی:
به توالی تقسیم جملات زیر در دنباله ی فیبوناچی توجه کنید:
Fn-1 Fn
2 | 3 | 1.5 | |
3 | 5 | 1.666666666… | |
5 | 8 | 1.6 | |
8 | 13 | 1.625 | |
… | … | … | |
144 | 233 | 1.618055556… | |
233 | 377 | 1.618025751.. |
مشاهده میشود که حاصل تقسیم به صورت مداوم به سمت نسبت طلایی میل میکند.
به بیان بهتر دنباله ی فیبوناچی به نسبت طلایی همگرا است.
بدیهی است که با تقسیم اعداد متوالی بزرگتر، نسبت طلایی با دقت بیشتری به دست می آید.
محاسبه ی جملات دنباله ی فیبوناچی با استفاده از نسبت طلایی:
رابطه ی جادویی دنباله ی فیبوناچی با نسبت طلایی همچنان ادامه دارد، تا جایی که میتوان برای بدست آوردن جملات دنباله از نسبت طلایی استفاده کرد.

میدانیم که برای بدست آوردن هر جمله ی فیبوناچی بایستی دو جمله قبلی آنرا با هم جمع کنیم.
اما فرمولی با استفاده از نسبت طلایی وجود دارد که به کمک آن میتوان هر جمله ی دنباله ی فیبوناچی را بدون نیاز به داشتن جملات ماقبل آن محاسبه کرده و بدست آورد.
کافیست برای بدست آوردن جمله ی n ام دنباله ی فیبوناچی، مقدار n را در فرمول بالا جایگذاری کنیم.
عددی که بدست می آید دقیقا برابر با مجموع دو جمله ی قبلی دنباله خواهد بود.
برای مثال برای محاسبه ی جمله ی ششم دنباله داریم:
که خیلی نزدیک به عدد 8 است.
همچنین میتوان هر جمله ی دنباله را از طریق ضرب کردن جمله ی ماقبل آن در نسبت طلایی بدست آورد.
برای این کار پس از انجام ضرب باید حاصل به دست آمده را گرد کنیم تا جمله ی بعدی دنباله حاصل شود.
*نکته: این روش فقط برای اعداد بعد از 1 کاربرد داد.
برای مثال برای محاسبه ی جمله ی بعد از عدد 8 در دنباله داریم:
8φ=8*1.618034…=12.94427
که پس از گرد کردن به مقدار 13 میرسیم که همان جمله ی هفتم دنباله است.
نسبت طلایی به عنوان شیب در معادله ی خط و یافتن نقاط فیبوناچی
معادله ی خط به صورت زیر تعریف میشود:
y=mx
که در آن m شیب خط مورد نظر و عددی حقیقی است.
در صورتی که m عددی گنگ باشد، از هیچ نقطه ای با مختصات صحیح به جز مبدا عبور نخواهد کرد.
در واقع امکان ندارد این خط از نقطه ای عبور کند که هم x و هم y آن نقطه عدد صحیح باشند.
حال خطی را در نظر بگیرید که شیب آن φ باشد.از آنجایی که φ عددی گنگ است، تنها نقطه ای که دارای مختصات صحیح است و این خط از آن عبور میکند مبدا است.
به همین خاطر نقطههایی را با x و y صحیح در نظر میگیریم که کمترین فاصله را از این خط دارند.
ابتدا به نظر میرسد نقطه (۱، ۱) کمترین فاصله را با این خط دارد؛ ولی فاصله نقطه (۲، ۱) از این خط کمتر هم هست. سپس متوجه میشویم که نقطه (۳، ۲) فاصله کمتری با این خط دارد.
همچنین فاصله نقطه (۵، ۳) از این هم کمتر است. این نقاط به همین ترتیب ادامه خواهند یافت و در زیر چند نقطه بعدی را که فاصلهشان از این خط کمتر میشود را میبینید:
(1,1),(1,2),(2,3),(3,5),(5,8)(8,13),(13,21),(21,34),(34,55),…
با کمی دقت در مختصات این نقاط به سادگی درمیابیم که این مختصات از الگوی دنباله فیبوناچی پیروی میکنند. این نقاط را نقاط فیبوناچی مینامند.
روز فیبوناچی:
در تقویم میلادی روز 23 نوامبر به نام روز فیبوناچی نامگذاری شده است.
دلیل انتخاب این روز این است که نمایش تاریخ آن در تقویم میلادی نشان دهنده ی چندین جمله ی ابتدایی دنباله ی فیبوناچی میباشد.(11/23)
دنباله ی فیبوناچی در طبیعت:

اصلا یاد گرفتن ریاضی به چه دردی میخورد؟
اگر این سوال مدت ها در ذهن شما بدون پاسخ باقی مانده است،در این بخش از مقاله قصد داریم به شما ثابت کنیم که نه تنها دنیای اطراف انسان،بلکه مغز ما نیز توسط ریاضیات تسخیر شده است!
اصطلاحا میگویند: اعداد فیبوناچی در طبیعت یافت میشوند.
منظور از این جمله این است که در الگوهای طبیعت به وفور از اعداد فیبوناچی استفاده شده است.
اما چرا؟؟؟
دلیل آن هم خیلی ساده وجود نسبت طلایی در دنباله ی فیبوناچی است.
جالب است بدانید مغز ما به گونه ای طراحی شده که وجود نسبت طلایی در دنیای اطراف باعث میشود همه چیز برایمان جذابتر جلوه کند.
کاربرد های دنباله فیبوناچی در زندگی روزه مره
به طور کلی نسبت طلایی در معماری، طراحی، نقاشی ، قطعات مشهور موسیقی یا حتی در جراحی های زیبایی کاربرد دارد.

– در بدن انسان هر چه نسبت اجزای مختلف صورت به نسبت طلایی نزدیک تر باشد، میزان زیبایی آن شخص بیشتر است.
به همین دلیل اغلب جراحان زیبایی از نسبت طلایی در جراحی های مختلف استفاده میکنند.
– در تمام آثار معماری بزرگ جهان مثل پارتنون یونان، تاج محل هندوستان، پرسپولیس ایران و حتی معماری سنتی ایران مثل عالی قاپو و مسجد امام از نسبت طلایی برای طراحی استفاده شده است.

هرچه نسبت طلایی در این آثار با دقت بیشتری به کار گرفته شود،میزان زیبایی و جذابیت آن از دید انسان بیشتر است.
– نقاش های بزرگ مثل لئوناردو داوینچی و سالوادور دالی نیز در آثار معروف خود نسبت طلایی را به کار برده اند.از نمونه نقاشی های مشهور میتوان به تابلوی مونالیزا و تابلوی شام آخر اشاره کرد.
– از نسبت طلایی همچنین در طراحی نوت های موسیقی استفاده میشود. موسیقی دانان بزرگی مثل باخ، موتزارت و بتهوون از عدد طلایی در فاصله گذاری بین نت ها استفاده می کردند.
یکی از بهترین نمونه ها، سمفونی شماره 5 بتهوون است که کاملا براساس عدد طلایی به وجود امده است. موتزارت نیز بسیاری از آثار خود، بهخصوص سوناتهای پیانو را بر اساس نسبت طلایی ساخته است.
– زنبورهای عسل نیز از بسیاری از جهات از اعداد دنباله ی فیبوناچی و نسبت طلایی پیروی میکنند.
واضح ترین مثال نسبت تعداد زنبورهای مادهی یک کندو بر تعداد زنبورهای نر است که معمولا عددی نزدیک به ۱٫۶۱۸، یعنی نسبت طلایی، است.
– تعداد گلبرگهای اکثر گل ها برابر با جملات دنباله ی فیبوناچی و نحوه ی چینش آنها نسبت به یکدیگر از نسبت طلایی پیروی میکند.

این آرایش عددی به برگ ها و گلبرگها و… اجازه میدهد تا به گونهای رشد کنند که حداکثر نور خورشید و باران را دریافت کنند، در بهترین زاویه نسبت به یکدیگر برای رشد و گلدهی قرار میگیرند و به این طریق گلبرگ ها برهم سایه نمی اندازند.
– بسیاری از برند های مشهور دنیا مانند اپل ، پپسی و توییتر در طراحی لوگوی خود از ارقام نسبت طلایی استفاده کرده اند.
– تعداد مارپیچ های گل آفتابگردان اغلب برابر با یک از اعداد فیبوناچی است.همچنین در نحوه ی چینش تخمههای آفتابگردان یا بسیاری از گونههای گیاهی دیگر، چینشی که از نسبت طلایی پیروی میکند درواقع ایدهآلترین حالت ممکن را به نمایش میگذارد تا در مرکز تراکم بیش از حد و در گوشهها تراکم کم ایجاد نشود.
و موارد بیشمار دیگری که استفاده از نسبت طلایی در آن ها بدون شک یکی از اصلیترین دلایل چشم نوازی ، منحصر به فرد بودن و ایده آل بودن آن ها است.
کاربرد اعداد فیبوناچی:
در این مقاله تا حد زیادی با کاربرد های مختلف اعداد فیبوناچی در حوزه های مختلف آشنا شدیم.اما شاید برجسته ترین کاربرد اعداد فیبوناچی را بتوان کاربرد آن در بورس و فارکس نامید.
از اعداد فیبوناچی همچنین در تحلیل تکنیکال (Technical Analysis) برای پیشبینی قیمت و ورود به بازار بورس اوراق بهادار، بازار ارز و فارکس و نیز بازارهای بورس کالا استفاده میشود.
تحلیلگران زیادی معتقدند به کمک ابزار فیبوناچی، از جمله فیبوناچی اصلاحی (retracement) و فیبوناچی انبساطی (extension)، میتوان رفتار بازار را در ۷۰ درصد موارد با موفقیت پیشبینی کرد.
تحلیلگران از این ابزار برای تعیین نقاط ورود و خروج و محاسبهی محدودهی حمایت یا مقاومت استفاده میکنند.
آنچه در این مقاله بررسی کردیم،تنها بخش کوچکی از شگفتی های موجود در دنیای ریاضیات است.
اگر به ارتباط عمیق و مستقیم ریاضی با دنیای اطراف مان پی ببریم،یاد گرفتن ریاضی برایمان بسیار لذت بخش تر خواهد بود.
گردآورنده : هانیه اکرمی





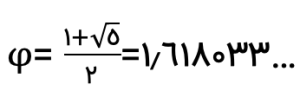
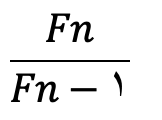
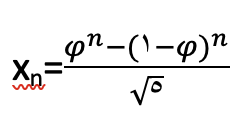
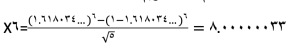
چقدر جالب 👍🏻👌🏻
ممنون از محتوای بینظیر تون